The world we live in is full of patterns that can be described with the help of mathematics. The rainbow in the sky, river meanders, shadows, spider web, honeycombs, pattern on animal fur, are just some of the natural phenomena that are based on mathematical principles. Mathematics is all around us and everything is number. The exhibition "Mathematics and Nature" was first shown at the event "May Month of Mathematics" organized by the Center of the Promotion of Science and the Mathematical Institute in Belgrade in 2013.
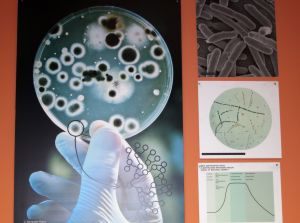
Bacterical Growth
Did you know that bacteria are the most numerous living organisms on our planet? Majority f bacterial species use fission for its reproduction during which one bacterial cell divides and gives two new cells. If division happens each hour and we start with only one bacterium, after only day there will be more than 16 million bacteria! Bacterical growth is exponential and can be presented with following equation:
Symmetry
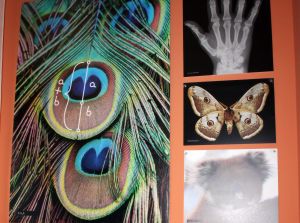
If you take a look in the mirror, you will see one of the most beautiful examples of bilateral symmetry! Symmetrical forms have plain, axis and center of symmetry. Maybe you have already noticed that some organisms do not have bilateral symmetry. Many of them show radial symmetry and have spherical or cylindical shapes.
Parallel Lines
Look around you and look carefully – ou will se the examples of parallelism almost everywhere, in flora and fauna. In geometry parallelism is the relation between two geometrical forms. Two lines are parallel if they are in the same plane and do not intersect.
Geometrical Forms
Did you know that bees are excellent mathematicians? They have chosen hexagon out of all possible forms as a pattern for building the honeycomb, because that way maximal usage of space and material can be achived. Another shape often seen in nature is ball – geometrical form contoured by sphere. It is also called "the perfect geometrical form" among mathematicians.
Golden Section
You will be surprised how easy one can spot the examples of golden ratio – the specific ration in which relation of two values added and the bigger value equals relation of bigger value to smaller value. This has often been called the "universal law".
Fibonacci Sequence
Petals of many types of flowers and leafs of numerous plants, hurricanes, galaxies, seeds of sunflower and human ear follow the same pattern. They all have a spiral shape that almost perfectly corresponds to the golden spiral known as the Fibonacci sequence.1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Each following number equals the sum of previous two.
Fractals
What do snowflakes, lightning, seashores, cauliflowers, tree branches, dendrites and mountain ranges have in commen? These are all great examples of natural fractals. Fractals are geometrical patterns, which can be disassembled into smaller one that are similar version of the big one.
Stripes
Isn't the nature the greatest artist of all? Almost all incredibly beautiful natural stripes and forms can be described by mathematical equations.
Spots and Patterns
Alan Turing got a brilliant idea how to use the mathematics and equations to describe the forming of beautiful patterns on hide, feathers and fur of animals. Imagine the embryo with two kinds of chemical compounds inside (activators and inhibitors) who interact among themselves and together influence the pigment to create numerous patterns. Activator concentration that changes in time is presented whit the equation:
